Quantum correlation functions through tensor network path integral

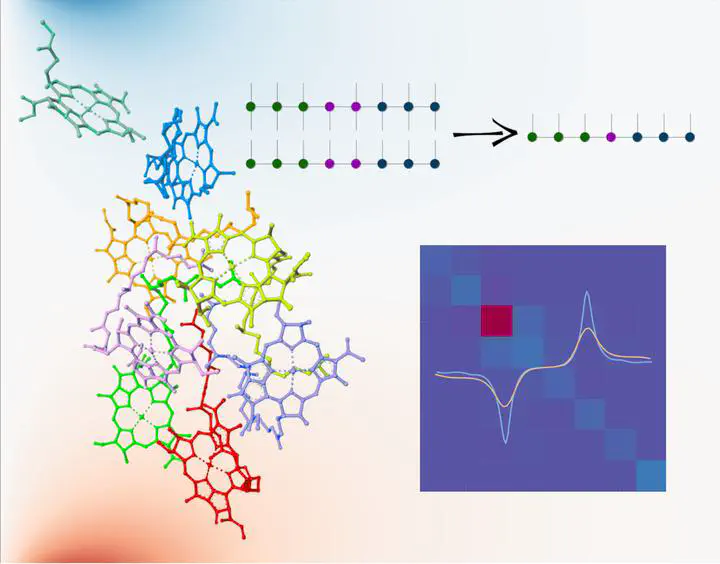
Abstract

Tensor networks have historically proven to be of great utility in providing compressed representations of wave functions that can be used for the calculation of eigenstates. Recently, it has been shown that a variety of these networks can be leveraged to make real time non-equilibrium simulations of dynamics involving the Feynman–Vernon influence functional more efficient. In this work, a tensor network is developed for non-perturbatively calculating the equilibrium correlation function for open quantum systems using the path integral methodology. These correlation functions are of fundamental importance in calculations of rates of reactions, simulations of response functions and susceptibilities, spectra of systems, etc. The influence of the solvent on the quantum system is incorporated through an influence functional, whose unconventional structure motivates the design of a new optimal matrix product-like operator that can be applied to the so-called path amplitude matrix product state. This complex-time tensor network path integral approach provides an exceptionally efficient representation of the path integral, enabling simulations for larger systems strongly interacting with baths and at lower temperatures out to longer time. The derivation, design, and implementation of this method are discussed along with a wide range of illustrations ranging from rate theory and symmetrized spin correlation functions to simulation of response of the Fenna–Matthews–Olson complex to light.