Rate Theory

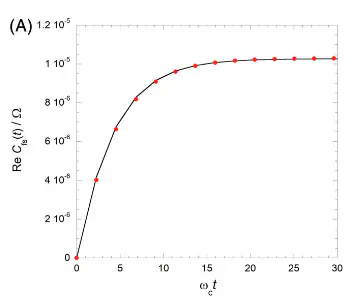
Rates are a corner-stone of chemistry. Most reactions are characterized by a single number — the rate. While classical theory of rates are still used, quantum mechanically, rate is related to the flux correlation function. It can be extracted as the value of the flux-side autocorrelation function, $$ C_f(t) = \frac{1}{Z_R}\text{Tr}\left[\,\exp\left(-\beta H\right)\,\hat{h}_R\,\hat{U}^\dagger\,\hat{F}\,\hat{U}\,\right], $$ when it plateaus. While this yields a single number representing the rate of the process, it completely misses out on the transients. Additionally, rate-theory fails to do justice to processes that have multiple time-scales. However, despite its short-comings, this is the best that one can do when the process is very slow. It is not possible to simulate the quantum dynamics when the reaction has a time-scale of a few milliseconds or nanoseconds.

Equilibrating the system along with the solvent is computationally challenging. We have shown that one can avoid computing the equilibrium correlation function at the cost of longer plateau times. As an added benefit, one gains further insights because this non-equilibrium formulation of rate enables analysis of the transients multiple time-scales.

For cases where the solvent needs to be described atomistically, we have also developed an approximate equilibration scheme which works with a variety of quantum-classical dynamics schemes and takes away some of the increased cost of doing the fully non-equilibrium simulations.