Multisite Tensor Network Path Integral
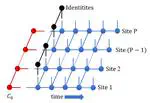
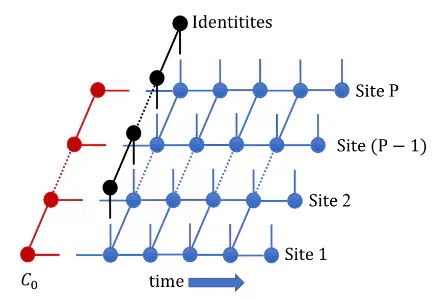 2D MS-TNPI network that is simultaneously decomposed along the temporal and spatial axes.
2D MS-TNPI network that is simultaneously decomposed along the temporal and spatial axes.Simulating the dynamics of a quantum system coupled to a dissipative environment gets challenging because of the non-Markovian memory that needs to be accounted for. While iterative propagation and basic tensor network path integral (TNPI) enable simulation of longer memory times, the dimensionalities of systems that can be simulated are still very limited. For extended systems the dimensionality grows exponentially with the number of sites or monomers, making these techniques untenable. Consider $50$ monomers described by two levels each. That implies that the Hilbert space has a dimensionality of $2^{50}$. This exponential growth of the dimensionality of the Hilbert space may be controlled if the dynamics can be restricted to a significantly smaller subspace. This is the case when considering the single particle subspace in a Frenkel-like process which conserves the number of particles. However, solving the 50-dimensional problem, while more feasible than the $2^{50}$ dimensional problem, is still a significant challenge.
The standard TNPI decomposes the path integral expression only along the temporal dimension. However, to account for these extended systems, one needs to decompose it also along a spatial dimension, separating out the individual sites. Thus a two-dimensional tensor network decomposition is achieved. Contraction of this 2D tensor network after incorporation of the influence functional yields the time-dependent reduced density operator corresponding to the extended system in the presence of a dissipative environment. The simulations happen in the full Hilbert space allowing for a transparent inclusion of more involved effects like multi-photon process, multi-dimensional spectra, etc.