Multidimensional Integrals using the Monte Carlo Technique

Metropolis Monte Carlo is a statistical technique that can be used to evaluate integrals of the following form: $$\int_{-\infty}^\infty P(\vec{x})\,g(\vec{x})\,d\vec{x},$$ where both $P(\vec{x})$ is a probability density $\mathbb{R}^d\to\mathbb{R}^+$ that satisfies $\int_{-\infty}^\infty P(\vec{x})d\vec{x} = 1$, and $g(\vec{x})$ is a function $\mathbb{R}^d\to\mathbb{R}$.

To start with let us implement the MC routine for a 1D case. A new point has to be generated at every step. The maximum amount by which this point can differ from the previous point is input as xmax in the following function.

function MCsingle(P, g, xmax::Float64, nsteps::Int64)
    x = rand() - 0.5
    gtot = g(x)
    p = P(x)
    accept = 1
    for _ = 1:nsteps - 1
        xnew = x + (2rand() - 1) * xmax
        pnew = P(xnew)
        if pnew / p ≥ rand()
            x = xnew
            p = pnew
            accept += 1
        end
        gtot += g(x)
    end
    gtot / nsteps, accept / nsteps
end

Write a function to calculate the error bar by dividing the nsteps MC steps into nblocks blocks and looking at the standard deviation between the simulations.

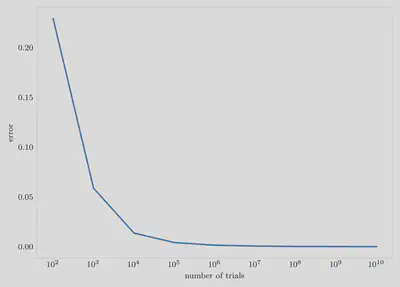
Now this function can be used to calculate the value of $\int_{-\infty}^\infty \frac{\exp(-x^2)}{\sqrt{\pi}} x^2 dx$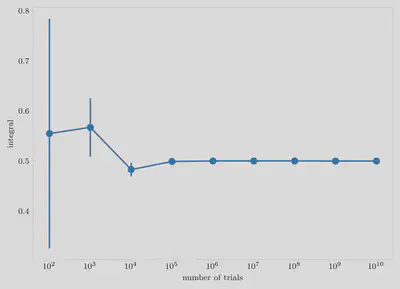

Extend the 1D MC function to account for multiple dimensions.