Bose Research Group


The Bose Research Group focuses on developing novel computational approaches to simulating non-equilibrium dynamics of quantum systems in the condensed phase, overcoming the curse of dimensionality.


    

Announcements

All announcements»

  • Postdoctoral, PhD and project positions are available in our group. Check out for more information about open positions.

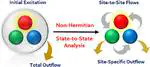
  • June 2025: Devansh Sharma’s non-Hermitian generalization of the state-to-state analysis method published in the Journal of Chemical Theory and Computation. Check it out…

  • March 2025: Our adaptive kink filtration technique for path integral simulations of open quantum systems published in the Journal of Chemical Physics. See more…

  • February 2025: Devansh Sharma presents his Masters’ project. Congratulations! Now on to even more exciting things! See more…

  • October 2024: Devansh Sharma’s exploration of the effect of loss mechanisms on linear spectra using our Path Integral Lindblad Dynamics method published in the Journal of Chemical Theory and Computation. Congratulations! Check it out…

Research Areas

The cost of simulations of time-evolution of quantum systems grows exponentially with the number of dimensions involved. Various approaches, both approximate and numerically exact, are required to make such simulations feasible. Explore the ideas that are being developed in the group.

*
All Path Integrals Applications Software
QuantumDynamicsCLI.jl

QuantumDynamicsCLI.jl

Simulating the dynamics of quantum systems is a challenging task with a multitude of complicated computational methods. The QuantumDynamicsCLI.jl package provides an application that leverages QuantumDynamics.jl to help making simulations a routine affair.

QuantumDynamics.jl

QuantumDynamics.jl

QuantumDynamics.jl is an open-source software for simulation of non-adiabatic dynamics of open quantum systems. Though written with performance in mind, QuantumDynamics provides a high throughput platform for experimentation with state-of-the-art approaches to method development.

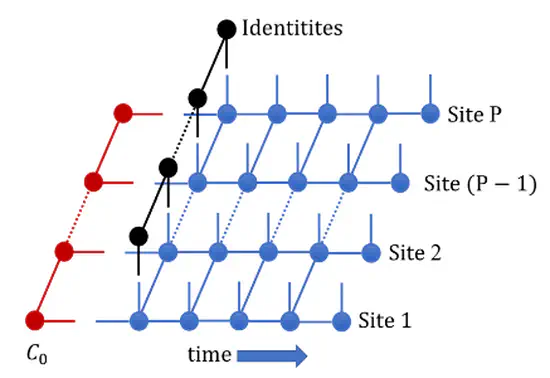
Multisite Tensor Network Path Integral

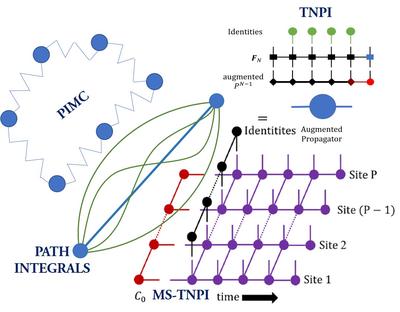
Multisite Tensor Network Path Integral

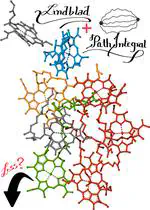
How does one handle the dynamics of extended quantum systems interacting with local dissipative media? MS-TNPI provides an answer to this problem by introducing a 2D tensor network decomposition of the path integral expressions.

Exciton Transport

Exciton Transport

COMING SOON

Tensor Network Path Integral

Tensor Network Path Integral

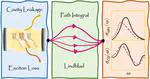
Simulating exact quantum dynamics of a low-dimensional system interacting with a large dissipative environment proves to be challenging due to presence of non-Markovian effects. Tensor networks can be successfully used to reduce the memory burden of these non-Markovian simulations making it possible to study chemical reactions in the condensed phase with greater accuracy.

Topics under Study

Adiabatic Switching Correlation Functions DMRG Exciton Transport Light-Harvesting Complex Lossy Systems Path Integrals Quantum-Classical Quasiclassical Rate Theory Routes of Transport Software Spin Chain Tensor Networks Transport Efficiency Wigner

Latest Publications

Search through all publications»

Adaptive Kink Filtration: Achieving Asymptotic Size-Independence of Path Integral Simulations Utilizing the Locality of Interactions
Path integral calculations scale exponentially with system sizes, making simulations of large systems prohibitively difficult. However, physical systems have certain constraints; interactions, for instance, are generally quite local. Is it possible to use these features to make the cost of path integral simulations indepedent of system size? Explore in depth…
PDF Cite Project DOI
Adaptive Kink Filtration: Achieving Asymptotic Size-Independence of Path Integral Simulations Utilizing the Locality of Interactions
Non-Hermitian State-to-State Analysis of Transport in Aggregates with Multiple Endpoints
Transport efficiency in aggregates is a complex many-body non-equilibrium phenomenon. Imagine a localized excitation generated at initial time. This localed excitation has to travel to the trap site and then would leak out. This total process would have a net time-scale. How does one calculate this emergent time-scale? What happens if there are multiple end-points?
PDF Cite DOI
Non-Hermitian State-to-State Analysis of Transport in Aggregates with Multiple Endpoints
Impact of Loss Mechanisms on Linear Spectra of Excitonic and Polaritonic Aggregates
Let’s study spectra for lossy systems! How would the line shapes be affected? How do we exactly quantify the impact of such changes? Our Path Integral Lindblad Dynamics method provides a perfect way of answering these questions. Walk with us while we explore these questions…
PDF Cite Project Project DOI
Impact of Loss Mechanisms on Linear Spectra of Excitonic and Polaritonic Aggregates
Incorporation of Empirical Gain and Loss Mechanisms in Open Quantum Systems through Path Integral Lindblad Dynamics
How does one incorporate loss and gain mechanisms determined by empirical time-scales in an otherwise numerically exact computation? One way is by combining Lindblad master equations with path integral simulations. Why would one do this? Where are the details? Read more to find out…
PDF Cite Project DOI
Incorporation of Empirical Gain and Loss Mechanisms in Open Quantum Systems through Path Integral Lindblad Dynamics
Quantum correlation functions through tensor network path integral
Tensors networks are now-a-days being used for simulating the non-equilibrium dynamics of open quantum systems. In this work, we introduce a novel tensor network approach to computing quantum correlation functions for open quantum systems using Feynman-Vernon influence function. Read in full detail…
PDF Cite Project DOI
Quantum correlation functions through tensor network path integral
See all publications